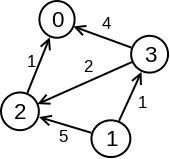
U problemima koji slede bavićemo se težinskim grafovima (engl. weighted graph), odnosno grafovima u kojima je svakoj grani pridružena njena težina (engl. weight). Umesto težina grane često ćemo koristiti i termin dužina grane i pod terminom dužina puta smatraćemo zbir dužina grana na tom putu (a ne broj grana na tom putu). Na slici 1 prikazan je jedan usmereni težinski graf. U ovom grafu dužina puta \((1,2,0)\) iznosi \(5+1=6\), dok dužina puta \((1,3,2,0)\) iznosi \(1+2+1=4\).

U programskom jeziku C++ težinski graf možemo predstaviti ili matricom povezanosti u kojoj se umesto logičkih vrednosti čuvaju težine grana (uz neku specijalnu numeričku vrednost koja označava da čvorovi nisu povezani) ili listama povezanosti, gde se u svakom elementu liste povezanosti čuva indeks krajnjeg čvora grane i težina grane. Ako težinski graf predstavljamo listama povezanosti i ako su dužine grana celobrojne, graf možemo deklarisati na sledeći način:
typedef int Cvor;
typedef int Tezina;
vector<vector<pair<Cvor, Tezina>>> listaSuseda(n);Novu granu \((cvorOd,cvorDo)\) težine \(t\) dodajemo u graf na sledeći način:
listaSuseda[cvorOd].emplace_back(cvorDo, t);Podsetimo se da se primenom funkcije emplace_back najpre konstruiše uređeni par čvora i njegove težine, a zatim taj uređeni par dodaje na kraj vektora.
Primer 2.8.1. Usmereni težinski graf sa slike 1 zadajemo listama povezanosti na sledeći način:
vector<vector<pair<Cvor, Tezina>>> listaSuseda
{{}, {{2,5}, {3,1}}, {{0,1}}, {{0,4}, {2,2}}};Ako je graf neusmeren, možemo ga smatrati usmerenim, pri čemu svakoj njegovoj neusmerenoj grani odgovaraju dve usmerene grane iste dužine, u oba smera. Algoritmi koje ćemo razmatrati nad težinskim grafovima odnose se i na usmerene i na neusmerene grafove.