Prilično je jasno da se zadatak može rešiti tako što se prebroje komponente povezanosti u grafu koji gradimo na osnovu podataka o lavirintu, međutim, prvo treba na pravi način definisati taj graf. Jedan način je da svaki kvadrat u lavirintu podelimo na četiri oblasti i da svaka oblast predstavlja jedan čvor grafa (taj graf ima \(4mn\) čvorova).
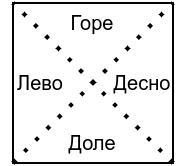
Oblasti u jednom kvadratu su povezane, osim ako je postavljena neka živa ograda.
- Iz gornje oblasti možemo doći u levu, osim ako je živa ograda na glavnoj dijagonali i u desnu, osim ako je živa ograda na sporednoj dijagonali.
- Iz donje oblasti možemo doći u levu, osim ako je živa ograda na sporednoj dijagonali i u desnu, osim ako je živa ograda na glavnoj dijagonali.
- Iz leve oblasti možemo doći u gornju, osim ako je živa ograda na glavnoj dijagonali i u donju, osim ako je živa ograda na sporednoj dijagonali.
- Iz desne oblasti možemo doći u gornju, osim ako je živa ograda na sporednoj dijagonali i u donju, osim ako je živa ograda na glavnoj dijagonali.
Mogući su prelasci i iz jednog u drugi kvadrat.
- Iz gornje oblasti bilo kog kvadrata možemo doći u donju oblast kvadrata iznad tog kvadrata (ako takav kvadrat postoji).
- Iz donje oblasti bilo kog kvadrata možemo doći u gornju oblast kvadrata ispod tog kvadrata (ako takav kvadrat postoji).
- Iz leve oblasti bilo kog kvadrata možemo doći u desnu oblast kvadrata levo tog kvadrata (ako takav kvadrat postoji).
- Iz desne oblasti bilo kog kvadrata možemo doći u levu oblast kvadrata desno od tog kvadrata (ako takav kvadrat postoji).
Na narednoj slici prikazana je povezanost oblasti u lavirintu koji se opisuje karakterima:
/\/ /
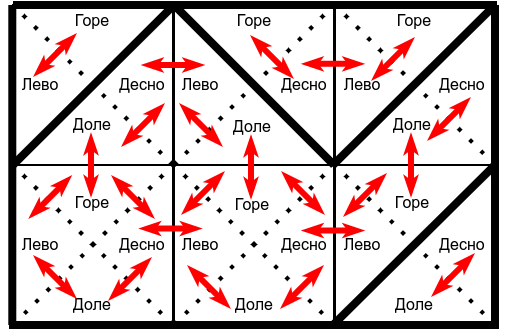
Odgovarajući graf je prikazan na narednoj slici.
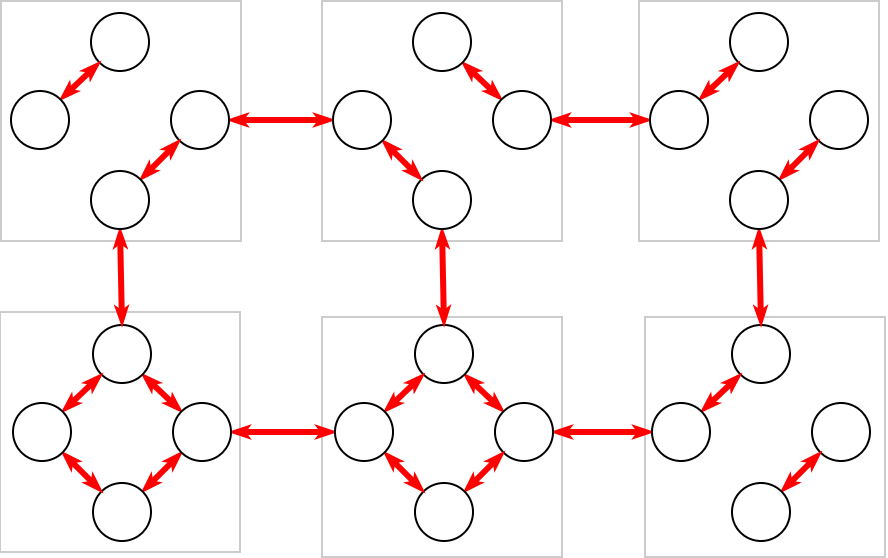
Pošto kvadrata ima \(m \times n\), čvorova grafa ima \(4 \times m \times n\). Svaki čvor je povezan sa najviše \(3\) druga čvora, pa je ukupna složenost prebrojavanja komponenti \(O(mn)\).
// svakom polju odgovaraju ima 4 čvora grafa
enum deo {GORE=0, DOLE, LEVO, DESNO};
// obilazak grafa zadatog nizom stringova od cvora sa koordinatama (v0, k0, d0)
// to je cvor u vrsti v0, koloni k0 i delu d0
// poseceni cvorovi su određeni visedimenzionim nizom posecen
void dfs(const vector<string>& linije, int m, int n,
vector<vector<vector<bool>>>& posecen,
int v0, int k0, int d0) {
// na steku cuvamo koordinate cvorova grafa
stack<tuple<int, int, int>> s;
s.emplace(v0, k0, d0);
posecen[v0][k0][d0] = true;
while (!s.empty()) {
// skidamo koordinate tekuceg cvora sa steka
int v, k, d;
tie(v, k, d) = s.top(); s.pop();
// odredjujemo susede tekuceg cvora (ima ih najvise 3)
vector<tuple<int, int, int>> susedi;
// analiziramo polozaj tekuceg cvora u njegovom polju
switch(d) {
case GORE:
// levi i desni cvor tekuceg polja (ako nisu zaklonjeni preprekama)
if (linije[v][k] != '\\')
susedi.emplace_back(v, k, LEVO);
if (linije[v][k] != '/')
susedi.emplace_back(v, k, DESNO);
// donji cvor polja iznad (ako to polje postoji)
if (v > 0)
susedi.emplace_back(v-1, k, DOLE);
break;
case DOLE:
// levi i desni cvor tekuceg polja (ako nisu zaklonjeni preprekama)
if (linije[v][k] != '/')
susedi.emplace_back(v, k, LEVO);
if (linije[v][k] != '\\')
susedi.emplace_back(v, k, DESNO);
// gornji cvor polja ispod (ako to polje postoji)
if (v < m-1)
susedi.emplace_back(v+1, k, GORE);
break;
// ...
}
// prolazimo kroz niz suseda tekuceg cvora
for (const auto& t : susedi) {
int vv, kk, dd;
tie(vv, kk, dd) = t;
// neposecene susede stavljamo na stek
if (!posecen[vv][kk][dd]) {
posecen[vv][kk][dd] = true;
s.push(t);
}
}
}
}
int main() {
// ucitavamo crtez lavirinta
int m, n;
cin >> m >> n;
string s;
getline(cin, s);
vector<string> linije(m);
string linija;
for (int i = 0; i < m; i++)
getline(cin, linije[i]);
// alociramo vektor posecenosti cvorova
// na pocetku nije posecen ni jedan cvor
vector<vector<vector<bool>>> posecen;
posecen.resize(m);
for (int i = 0; i < m; i++) {
posecen[i].resize(n);
for (int j = 0; j < n; j++)
posecen[i][j].resize(4, false);
}
// odredjujemo komponente povezanosti grafa i ispisujemo njihov broj
int brojOblasti = 0;
for (int v = 0; v < m; v++)
for (int k = 0; k < n; k++)
for (int d = GORE; d <= DESNO; d++)
if (!posecen[v][k][d]) {
dfs(linije, m, n, posecen, v, k, d);
brojOblasti++;
}
cout << brojOblasti << endl;
return 0;
}#include <iostream>
#include <string>
#include <vector>
#include <stack>
#include <tuple>
using namespace std;
// svakom polju odgovaraju ima 4 čvora grafa
enum deo {GORE=0, DOLE, LEVO, DESNO};
// obilazak grafa zadatog nizom stringova od cvora sa koordinatama (v0, k0, d0)
// to je cvor u vrsti v0, koloni k0 i delu d0
// poseceni cvorovi su određeni visedimenzionim nizom posecen
void dfs(const vector<string>& linije, int m, int n,
vector<vector<vector<bool>>>& posecen,
int v0, int k0, int d0) {
// na steku cuvamo koordinate cvorova grafa
stack<tuple<int, int, int>> s;
s.emplace(v0, k0, d0);
posecen[v0][k0][d0] = true;
while (!s.empty()) {
// skidamo koordinate tekuceg cvora sa steka
int v, k, d;
tie(v, k, d) = s.top(); s.pop();
// odredjujemo susede tekuceg cvora (ima ih najvise 3)
vector<tuple<int, int, int>> susedi;
// analiziramo polozaj tekuceg cvora u njegovom polju
switch(d) {
case GORE:
// levi i desni cvor tekuceg polja (ako nisu zaklonjeni preprekama)
if (linije[v][k] != '\\')
susedi.emplace_back(v, k, LEVO);
if (linije[v][k] != '/')
susedi.emplace_back(v, k, DESNO);
// donji cvor polja iznad (ako to polje postoji)
if (v > 0)
susedi.emplace_back(v-1, k, DOLE);
break;
case DOLE:
// levi i desni cvor tekuceg polja (ako nisu zaklonjeni preprekama)
if (linije[v][k] != '/')
susedi.emplace_back(v, k, LEVO);
if (linije[v][k] != '\\')
susedi.emplace_back(v, k, DESNO);
// gornji cvor polja ispod (ako to polje postoji)
if (v < m-1)
susedi.emplace_back(v+1, k, GORE);
break;
case LEVO:
// donji i gornji cvor tekuceg polja (ako nisu zaklonjeni preprekama)
if (linije[v][k] != '/')
susedi.emplace_back(v, k, DOLE);
if (linije[v][k] != '\\')
susedi.emplace_back(v, k, GORE);
// desni cvor polja levo (ako to polje postoji)
if (k > 0)
susedi.emplace_back(v, k-1, DESNO);
break;
case DESNO:
// donji i gornji cvor tekuceg polja (ako nisu zaklonjeni preprekama)
if (linije[v][k] != '\\')
susedi.emplace_back(v, k, DOLE);
if (linije[v][k] != '/')
susedi.emplace_back(v, k, GORE);
// levi cvor polja desno (ako to polje postoji)
if (k < n-1)
susedi.emplace_back(v, k+1, LEVO);
break;
}
// prolazimo kroz niz suseda tekuceg cvora
for (const auto& t : susedi) {
int vv, kk, dd;
tie(vv, kk, dd) = t;
// neposecene susede stavljamo na stek
if (!posecen[vv][kk][dd]) {
posecen[vv][kk][dd] = true;
s.push(t);
}
}
}
}
int main() {
// ucitavamo crtez lavirinta
int m, n;
cin >> m >> n;
string s;
getline(cin, s);
vector<string> linije(m);
string linija;
for (int i = 0; i < m; i++)
getline(cin, linije[i]);
// alociramo vektor posecenosti cvorova
// na pocetku nije posecen ni jedan cvor
vector<vector<vector<bool>>> posecen;
posecen.resize(m);
for (int i = 0; i < m; i++) {
posecen[i].resize(n);
for (int j = 0; j < n; j++)
posecen[i][j].resize(4, false);
}
// odredjujemo komponente povezanosti grafa i ispisujemo njihov broj
int brojOblasti = 0;
for (int v = 0; v < m; v++)
for (int k = 0; k < n; k++)
for (int d = GORE; d <= DESNO; d++)
if (!posecen[v][k][d]) {
dfs(linije, m, n, posecen, v, k, d);
brojOblasti++;
}
cout << brojOblasti << endl;
return 0;
}